
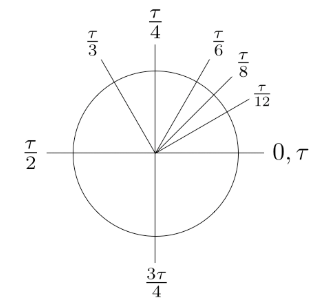
오일러 상수와 타우를 통하여 복소평면 원 안에 e^(iθ)로 쉽게 표현할 수 있고,
이를 통해 3차원 complex_output의 sample_rate(signal_source)를 정할수 있다.
'etc > Math' 카테고리의 다른 글
| Elementary Number Theory (1학기 ) (0) | 2020.07.29 |
|---|---|
| 복소평면의 내적 (0) | 2020.07.29 |


오일러 상수와 타우를 통하여 복소평면 원 안에 e^(iθ)로 쉽게 표현할 수 있고,
이를 통해 3차원 complex_output의 sample_rate(signal_source)를 정할수 있다.
| Elementary Number Theory (1학기 ) (0) | 2020.07.29 |
|---|---|
| 복소평면의 내적 (0) | 2020.07.29 |
Chapter 1.1
Mathematical Induction >> 제 2 수학적 귀납법 >> 1일때 성립하는거 확인, n일때 성립한다고 가정했을때 n+1일때도 성립한다는 것을 보여라.
Theorem 1.1
Archimedean Property >> 아르키메데스 성질 >> 대수적 집합 내에선 무한히 크거나 무한히 작은 원소가 없다.
Theorem 1.2
First Principle of Finite Induction >> 제 1 수학적 귀납법 >> 제 2 수학적 귀납법에서 n을 최소의 자연수인 1이상의 아무 수로 설정.
Chapter 1.2
The Binomial Theorem >> 이항정리 (안함)
Chapter 2.1
Early Number Theory >> 정수론
Chapter 2.2
The Division Algorithm >> 나눗셈정리 >> a = bq + r 일때 q와 r이 유일하게 존재한다.
Theorem 2.1
Division Algorithm >> 나눗셈정리
Chapter 2.3
The Greatest Common Divisor >> 최대공약수
Def 2.1 >> a | b 기호 설명
Theorem 2.2
(a) a | 0, 1 | a, a | a
(b) a | 1 >> 무조건 a= ±1.
(c) a | b & c | d >> ac | bd
(d) a | b & b | c >> a | c
(e) a | b & b | a >> 무조건 a = ±b
(f) a | b (b ≠ 0) >> |a| ≤ |b|
(g) a | b & a | c <~> a | (bx + cy) (x, y는 임의의 정수)*******************************
Def 2.2
0이 아닌 정수 a, b에 대하여 양의 정수 gcd(a, b) = d라 할때, d는 다음을 따른다.
(a) d | a & d | b. (최대공약수임으로 당연한 성질)
(b) 정수 c에 대하여 c | a & c | b 이면 c ≤ d이다. ('최대'공약수가 d이므로 공약수 c는 d 보다 작거나 같아야 한다)
Theorem 2.3
0이 아닌 정수 a, b에 대하여 다음을 만족하는 정수 x, y 는 반드시 존재한다. (gcd(a, b) = ax + by)*******************
Theorem 2.3을 이용한 추론
집합 T = {ax + by | x, y 는 정수} 는 gcd(a, b)의 배수이다.***************
Def 2.3
0이 아닌 정수 a, b에서 gcd(a, b) = 1 이면 a와 b는 서로소이다.
Theorem 2.4
0이 아닌 정수 a, b에 대하여 "a와 b가 서로소" <~> "ax + by = 1 을 만족하는 정수 x, y 존재"****************
Theorem 2.4를 이용한 추론 1
gcd(a, b) = d <~>gcd(a/d, b/d) = 1******************
Theorem 2.4를 이용한 추론 2
gcd(a, b) = 1일때, a | c & b | c >> ab | c (a와 b는 서로소임으로 당연한 말)
Theorem 2.5
Euclid's lemma(유클리드 보조 정리) >> gcd(a, b) = 1일때 a | bc >> a | c (a와 b는 서로소이니깐 당연)
Theorem 2.6
0이 아닌 정수 a, b에 대하여 정수 d = gcd(a, b)라 하면 <~> d | a & d | b (d는 최대'공'약수니깐)
<~> c | a & c | b >> c | d(d는 '최대'공약수이므로, 최대공약수는 공약수로 나눌 수 있다.)
Chapter 2.4
The Euclidean Algorithm >> 유클리드 호제법(2개의 자연수 또는 정식의 '최대공약수를 구하는' 알고리즘)
Lemma(보조정리)
a = qb + r >> gcd(a, b) = gcd(b, r) >>*******************(계산할때 한칸씩 땡기는 걸로 기억)
Theorem 2.7
k가 양수의 정수이면, gcd(ka, kb) = k gcd(a, b) (gcd안의 두 수가 공약수를 가지고 있으면 묶어서 밖으로 뺄 수 있다)**********
Theorem 2.7을 이용한 추론
0이 아닌 모든 정수 k에 대하여 gcd(ka, kb) = |k|gcd(a, b)이다.*******************
Def 2.4
0이 아닌 두 정수 a, b에 대하여 '최소공배수'는 lcm(a, b)로 표기하고, lcm(a, b) = m 이라고 할 때 다음 조건을 만족하는 0이 아닌 정수 m 은 반드시 존재한다.
(a) a | m & b | m
(b) a | c & b | c (c>0) >> m ≤ c (m은 a, b의 '최소'공배수 이므로 당연한 말)
Theorem 2.8
양의 정수 a, b에 대하여 gcd(a, b) x lcm(a, b) = ab 이다.
Theorem 2.8을 이용한 추론
어떠한 양의 정수 a, b에 대하여 lcm(a, b) = ab인 경우는 a, b가 서로소일때 이다.
Chapter 2.5
The Diophantine Equation ax + by = c (디오판토스 방정식)(정수인 해만 가지는 부정방정식)(안함)
Chapter 3.1 (Primes And Their distribution)(안함)
Chapter 3.2 (The Sieve of Eratosthenes)(에라토스테네스의 체)(안함)
Chapter 3.3 (The Goldbach Conjecture)(골드바흐의 추측)(안함)
Chapter 4 (합동 이론)
Chapter 4.1
Carl Friedrich Gauss (가우스)
Chapter 4.2
Basic Properties of Congruence (합동의 기본 속성)
Def 4.1 n을 고정된 양의 정수라 할때, 두 정수 a, b에 대하여 a-b(b-a)가 n으로 나누어 진다면, a ≡ b (mod n)으로 표기하고, a - b = kn이다.(k는 정수)
Theorem 4.1
임의의 두 정수 a, b에 대하여, a ≡ b (mod n) <~> a, b 가 n으로 나눴을때 음이아닌 같은 나머지를 가진다.
Theorem 4.2
n > 1 로 고정하고, a, b, c, d가 임의의 정수일때 다음을 만족한다.
(a) a ≡ a (mod n)
(b) a ≡ b (mod n) >> b ≡ a (mod n)
(c) a ≡ b (mod n) & b ≡ c (mod n) >> a ≡ c (mod n)
(d) a ≡ b & c ≡ d (mod n) >> a + c ≡ b + d & ac ≡ bd (mod n)
(e) a ≡ b (mod n) >> a + c ≡ b + c (mod n) & ac ≡ bc (mod n)
(f) a ≡ b (mod n) >> a^k ≡ b^k (mod n) (k는 양의 정수)
Theorem 4.3
ca ≡ cb (mod n) >> a ≡ b (mod n/d) (d = gcd(c, n) )
Theorem 4.3을 이용한 추론 1
ca ≡ cb (mod n) & gcd(c, n) = 1 >> a ≡ b (mod n)
Theorem 4.3을 이용한 추론 2
ca ≡ cb (mod p) & c가 p로 나누어 지지 않는다 (p는 소수) >> a ≡ b (mod p)
Chapter 4.3
Binary and Decimal representations of integers (2진 소수의 정수표현)(안함)
Chapter 4.4
Linear Congruences and the Chinese Remainder Therorem (선형합동과 중국인 나머지정리)
Theorem 4.7
선형합동 ax ≡ b (mod n) 는 d | b일때 근을 가진다.(d = gcd(a, n) ), d | b 이면, d개의 근을 가진다.(mod n으로 계산할때)
Theorem 4.7을 이용한 추론
gcd(a, n) = 1이면, 선형합동식 ax ≡ b (mod n) 은 오직 하나의 근을 가진다. (mod n으로 계산할때)
Theorem 4.8
Chinese Remainder Theorem (중국인 나머지 정리) >> 양의 정수이고, gcd(n(i), n(j) )= 1인 n(1), n(2), n(3), ... , n(r) 이 있을 때, 선형합동식 x ≡ a(1) (mod n(1) ) / x ≡ a(2) (mod n(2) ) / ... / x ≡ a(r) (mod n(r) )은 modulo n(1)n(2)n(3)...n(r) 에 대하여 오직 하나의 근을 가진다. { modulo 가 소수의 곱으로 이루어져 있을때)
Theorem 4.9
선형합동식 ax + by ≡ r (mod n), cx + dy ≡ s (mod n) 은 gcd(ad - bc, n) = 1일때 mondulo n 에 대하여 항상 하나의 근을 가진다.(안함)
Chapter 5
Fermat's Theorem (페르마의 정리)
Chapter 5.2
Fermat's Little Theorem And Pseudoprimes (페르마의 소정리)
//위키백과 참조
소수 p, 정수 a에 대하여 a^p ≡ a (mod p) {(a^p-1 ≡ 1)}
Theorem 5.1
Fermat's theorem (페르마의 정리)
소수 p를 a를 나누지 않는 수로 정의할때, a^p-1 ≡ 1 (mod p)
Theorem 5.1을 이용한 추론
소수 p에 대하여 a^p ≡ a (mod p) (a는 정수)
Theorem 5.1의 보조정리
서로 다른 두 소수 p, q에 대하여 a^p ≡ a (mod q) & a^q ≡ a (mod p) >> a^pq ≡ a (mod pq)
Theorem 5.2
n이 2가 아닌 유사소수일때, M(n) = 2^n - 1 은 n보다 큰 유사소수이다.(안함)
Theorem 5.3
n이 제곱수를 인수로 가지지 않는 합성수이고, p(i)를 서로 다른 소수라 했을때 n = p(1)p(2)...p(r)이라 하면 n은 absolute 유사소수이다.(안함)
Chapter 5.3
Wilson's Theorem (윌슨의 정리)
Theorem 5.4
소수 p에 대하여 (p-1)! ≡ -1 (mod p)
Theorem 5.5
이차합동식 x^2 + 1 ≡ 0 (mod p)(p는 2를 제외한 소수) 은 p ≡ 1 (mod 4) 일 때 반드시 근을 가진다.(안함)
Theorem 5.4
The fermat-kraitchik factorization method (안함)
Chapter 6
Number-Theoretic functions (수론적 함수)
Chapter 6.1
The sum and number of divisors (합과 약수의 개수)
Def 6.1
양의 정수 n에 대하여 τ(n)은 n의 모든 양의 약수를 가르키고 σ(n)은 이 약수들의 합을 가르킨다.
Theorem 6.1
n = p(1)^k(1) p(2)^k(2) p(3)^k(3) ... p(r)^k(r) 이 n>1일때의 소인수분해한 형태일때, n의 양의 약수 d 는 p(1)^a(1) p(2)^a(2) ... p(r)^a(r) (0 ≤ a(i) ≤ k(i) __i = 1, 2, 3, ..., r) 의 형태를 가진다.
Theorem 6.2
n = p(1)^k(1) p(2)^k(2) ... p(r)^k(r) 일때
τ(n) = (k(1) + 1)(k(2) + 1)(k(3) + 1)...(k(r) + 1) (모든 약수의 개수)
σ(n) = [{p(1)^(k(1) + 1) - 1} / p(1) - 1 ] [{p(2)^(k(2) + 1) - 1} / p(2) - 1 ] ... [{p(r)^(k(r) + 1) - 1} / p(r) - 1 ] (모든 약수의 합)
Def 6.2
수론적 함수 f가 f(mn) = f(m)f(n)을 만족시키면 곱셈적 함수라 부른다.
Theorem 6.3
τ함수와 σ함수는 모두 곱셈적 함수이다.
Theorem 6.4
곱셈적 함수 f에 대하여 함수 F(n) = Σ(d | n) f(d) 일때 함수 F(n)또한 곱셈적 함수이다.
Theorem 6.4를 이용한 추론
함수 σ와 τ는 곱셈적 함수이다. (F(n) = Σ(d | n) f(d) 만족)
Chapter 6.2
The Mobius inversion formula (뫼비우스 반전 공식)(안함)
Chapter 6.3
The Greatest integer function (가우스 함수) (안함)
Chapter 6.4
An application to the calendar (달력에 적용) (안함)
Chapter 7
Euler's Generalization of fermat's theorem (페르마 정리에 대한 오일러의 일반화)
Chapter 7.1
Leonhard Euler (오일러)
Chapter 7.2
Euler's phi-function (오일러 피 함수)ϕ
Def 7.1
n ≥ 1 일때, ϕ(n) 은 n을 넘지않고 양의 정수이면서 n과 서로소인 수를 나타낸다.
Theorem 7.1
소수 p에 대하여 k가 양수이면 ϕ(p^k) = p^k - p^(k-1)
Theorem 7.1의 보조정리
정수 a, b, c에 대하여 gcd(a, bc) = 1 <~>gcd(a, b) = 1 & gcd(a, c) = 1
Theorem 7.2 함수 ϕ는 곱셈적 함수이다.
Theorem 7.3 1보다 큰 정수 n = p(1)^k(1) p(2)^k(2) ... p(r)^k(r) 로 소인수분해된 형태를 가질때, ϕ(n) = (p(1)^k(1) - p(1)^k(1)-1) (p(2)^k(2) - p(2)^k(2)-1) ... (p(r)^k(r) - p(r)^k(r)-1)
Theorem 7.4 n > 2 에서 ϕ(n) 은 짝수인 정수이다.
Chapter 7.3
Euler's theorem (오일러 정리)
보조정리
n > 1 이고 gcd(a, n) = 1 일때, 양의 정수 a(1), a(2), ... , a(ϕ(n)) 가 n보다 작고 n과 서로소인 수 이면, aa(1), aa(2), aa(3), ... , aa(ϕ(n))은 a(1), a(2), ... , a(ϕ(n)) 에 대하여 modulo n으로 합동이다.
Theorem 7.5
1보다 크거나 같은 정수 n에 대하여 gcd(a, n) = 1 >> a^ϕ(n) ≡ 1 (mod n)
Theorem 7.5를 이용한 추론
p가 소수이고 a를 나눌 수 없을때, a^p-1 ≡ 1 (mod p)
Chapter 7.4
Some Properties of the phi-function (피-함수에 대한 성질)
Theorem 7.6
n ≥ 1인 각각의 정수 n에 대하여 n = ∑(d | n) ϕ(d) 의 합은 n의 모든 양의 약수로 확장된다.
Theorem 7.7
1보다 큰 n에 대하여 n보다 작은 양의 정수들의 합과 n과 서로소인 수는 1/2(nϕ(n)) 이다.(안함)
Theorem 7.8 (안함)
Chapter 8
Primitive Roots And Indices (원시근과 지수)
Chapter 8.1
The order of an Integer Modulo n ( modulo n일때 정수에 대한 위수)
Def 8.1
n > 1 이고 gcd(a, n) = 1 일때, modulo n에 대한 위수는 a^k ≡ 1 (mod n)을 만족시키는 가장 작은 양의 정수k 이다.
Theorem 8.1
정수 a가 modulo n에 대하여 k를 위수로 가진다 했을때, a^h ≡ 1 (mod n) <~> k | h (particular, k | ϕ(n) )
Theorem 8.2
정수 a가 modulo n에 대하여 k를 위수로 가질때, a^i ≡ a^j (mod n) <~> i ≡ j (mod k)
Theorem 8.3
a가 modulo n에 대하여 k를 위수로 가질때(h>0), a^h 는 modulo n에 대하여 k/gcd(h, k)를 위수로 가진다.
Theorem 8.3을 이용한 추론
a가 modulo n에 대하여 k를 위수로 가진다 할 때, a^h또한 gcd(h, k) = 1이면 k를 위수로 가진다.
Def 8.2
gcd(a, n) = 1 & ϕ(n)가 modulo n에 대하여 a의 위수일때 a를 정수n에 대한 원시근이라 부른다.
Theorem 8.4
gcd(a, n) = 1 이고 a(1), a(2), ... , a(ϕ(n))이 n보다 작은 양의 정수이면서 n과 서로소이라 하자. 만약 a가 n에대한 원시근이라면, a^1, a^2, a^3, ... , a^ϕ(n) 이 modulo n에 대하여 a(1), a(2), a(3), ... , a(ϕ(n))과 합동이다.
Theorem 8.4를 이용한 추론
def 8.2 의 n이 원시근이라면, theorem 8.4 의 원시근은 ϕ(ϕ(n))이다.
//역원//
a x a^-1 ≡ 1 (mod m) 을 만족하는 a^-1은 정수 a를 m으로 나눈 나머지 연산의 곱셈역원
(단, a와 m은 서로소)
///////////////////////////
Chapter 8.2
Primitive roots for primes (소수에 대한 원시근)
Theorem 8.5
| 복소평면에서 타우(τ)와 오일러상수(e)의 사용 (0) | 2020.07.29 |
|---|---|
| 복소평면의 내적 (0) | 2020.07.29 |

벡터공간에 따라 i는 스칼라로 생각.
(벡터의 기울기로 생각해도 무관)
| 복소평면에서 타우(τ)와 오일러상수(e)의 사용 (0) | 2020.07.29 |
|---|---|
| Elementary Number Theory (1학기 ) (0) | 2020.07.29 |